What is autocorrelation?
Autocorrelation is a statistical test that determines whether a random number generator is producing independent random numbers in a sequence.
What does autocorrelation test?
- The tests for autocorrelation are concerned with the dependence between numbers in a sequence.
- The test computes the autocorrelation between every m numbers (m is also known as the lag) starting with the ith number (i is also known as the
index).
What does autocorrelation look like?
Here is a list of random integers generated. See if you can identify a pattern by looking at the values in the sequence.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.63 | 0.28 | 0.30 | 0.42 | 0.97 | 0.05 | 0.71 | 0.63 | 0.17 | 1.0 |
| 0.61 | 0.19 | 0.94 | 0.64 | 0.84 | 0.54 | 0.56 | 0.57 | 0.09 | 0.99 |
| 0.01 | 0.10 | 0.69 | 0.38 | 0.93 | 0.85 | 0.68 | 0.14 | 0.18 | 0.84 |
| 0.19 | 0.71 | 0.44 | 0.72 | 0.95 | 0.28 | 0.96 | 0.51 | 0.50 | 0.89 |
| 0.66 | 0.31 | 0.50 | 0.33 | 0.89 | 0.54 | 0.73 | 0.76 | 0.62 | 0.92 |
If you look carfully at the following table of random integers generated, you'll notice that every number in the 5th, 10th, 15th, and 20th postion is
a
larger value.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.63 | 0.28 | 0.30 | 0.42 | 0.97 | 0.05 | 0.71 | 0.63 | 0.17 | 1.0 |
| 0.61 | 0.19 | 0.94 | 0.64 | 0.84 | 0.54 | 0.56 | 0.57 | 0.09 | 0.99 |
| 0.01 | 0.10 | 0.69 | 0.38 | 0.93 | 0.85 | 0.68 | 0.14 | 0.18 | 0.84 |
| 0.19 | 0.71 | 0.44 | 0.72 | 0.95 | 0.28 | 0.96 | 0.51 | 0.50 | 0.89 |
| 0.66 | 0.31 | 0.50 | 0.33 | 0.89 | 0.54 | 0.73 | 0.76 | 0.62 | 0.92 |
What are the important variables to remember?
m - is the lag, the space between the numbers being tested.
i - is the index, or the number in the sequence that you start with
N - the number of numbers generated in a sequence
M - is the largest integer such that 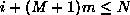
Mathematical Stuff
The test described below requires the computation of the autocorrelation between every m numbers (m is the lag) starting with the ith number. The
autocorrelation 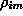 between the following numbers between the following numbers 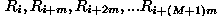 . .
The value M is is the largest integer such that 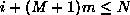 , where N is the total numbers in the sequence. Since a nonzero
autocorrelation implies a lack of independence, the following two-tailed test is appropriate: , where N is the total numbers in the sequence. Since a nonzero
autocorrelation implies a lack of independence, the following two-tailed test is appropriate:
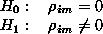
For large values of M, the distribution of the estimator of 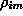 , denoted with a hat, is approximately normal if the values , denoted with a hat, is approximately normal if the values 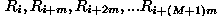 are uncorrelated. Then the test statistic can be formed as follows: are uncorrelated. Then the test statistic can be formed as follows:

which is distributed normally with a mean of zero and a variance of 1, under the assumption of independence, for large M.
The formula for 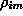 (with a hat), in a slightly different form, and the standard deviation of the estimator, (with a hat), in a slightly different form, and the standard deviation of the estimator, 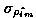 are as follows (Scmidt and Taylor 1970): are as follows (Scmidt and Taylor 1970):
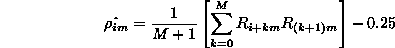
and

After computing 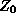 , do not reject the null hypothesis of independence if , do not reject the null hypothesis of independence if 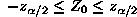 , where , where 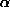 is the level of signifigance. If is the level of signifigance. If 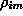 > 0, the subsequence is said to exhibit positive autocorrelation.
On the other hand, if > 0, the subsequence is said to exhibit positive autocorrelation.
On the other hand, if 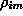 < 0, the subsequence is exhibiting negative autocorrelation, which means the m values are followed
by greater values. < 0, the subsequence is exhibiting negative autocorrelation, which means the m values are followed
by greater values.
How do you figure out the value of M?
To figure out the value of M, you must use some simple algebra. For example, the equation: 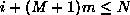 must be solved using the
given
values i the index, N the number of elements in the sequence, and m the lag. must be solved using the
given
values i the index, N the number of elements in the sequence, and m the lag.
For example:
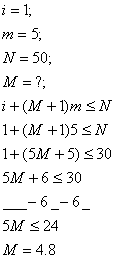
Since the value M must be an integer, the 0.8 is truncated and the 4 is saved as the value of M. Thus, M is equal to 4.
Using the Equations
To use the estimator equation, denoted 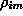 with a hat, you must understand the sequence and summation notations. The formula
is actually quite easy to use. with a hat, you must understand the sequence and summation notations. The formula
is actually quite easy to use.
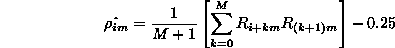
After identifying the index in the sequence, you start there by taking that value and multiplying by the value of the next number (index (i) + the
lag (m)). For the next number, you use the previous (i+m) and multiply that with the next value (i+m+m). This process continues iteratively
resulting in a sequence. The results of each multiplication are added together (this represents the summation).

The next equation is even simpler to use. After solving for M, plug the numbers in and use the results.
Applet for computing an Autocorrelation test
How to use the java autocorrelation applet
To use the Java autororrelation applet, place the supposed random numbers inside the text area by copying and pasting. After you have completed this,
input the lag (m) and the index (i). The rest of the values are calculated wihtin the applet and are not editable. Proceed by pressing the process
button. If you enter a non-numeric values for any of the fields, you will recieve and error notice and have to refresh the browser.
Special values:
Pim - the estimator that is approxomitely normal, denoted: 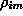
Qpim - the standard deviation of the estimator, denoted: 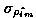
N- the number of elements in the sequence
M - is the largest integer such that 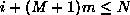
This applet only tests for an alpha value, denoted: 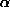 of 0.05, which is divided in a two-tailed test. The Z0 is
displayed in the test area after pressing the process button, along with an answer as to whether the test passes or fails. of 0.05, which is divided in a two-tailed test. The Z0 is
displayed in the test area after pressing the process button, along with an answer as to whether the test passes or fails.
Download Source Code for Applet
Drawbacks when using autocorrelation
- Autocorrelation is not very sensitive to small values of M, when the values being tested are on the low side. For example, if all the values were
equal to zero, then the resulting value would be -1.95, which is not enough to reject the hypothesis.
- Many sequences can be formed in a set of date (the sequence of all numbers, the sequence from the first, fifth, ..., numbers and so forth. If the
alpha is equal to 0.05, then there is a possibility of rejecting a true hypothesis. For example, if these are 10 independent events, the possibility
of finding of finding no autocorrelation alone is (0.95)10 or 0.60. Thus, 40% of the time signifigant autocorrelation would be detected
when it does not exist.
The Conclusion
When using autocorrelation tests, be cautious. Autocorrelation may be detected after numerous tests even when no autocorrelation exists.
|
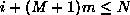
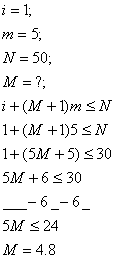

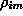 between the following numbers
between the following numbers 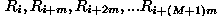 .
.
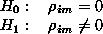

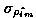 are as follows (Scmidt and Taylor 1970):
are as follows (Scmidt and Taylor 1970):
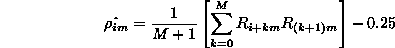
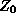 , do not reject the null hypothesis of independence if
, do not reject the null hypothesis of independence if 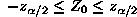 , where
, where 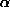 is the level of signifigance. If
is the level of signifigance. If